最初に時差の基本を確認しておきます。 　これは地球を上（北極側）から見た図です。 ↓次へ
	地球は２４時間で１回転しています。１回転＝３６０°ですから、１時間に１５°です。 　逆に言えば、経度で１５°離れると、１時間の時差がある、ということです。 ↓次へ　　↑もどる
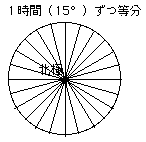
	経度１５°ずつ区切ってみると、２４分割できます。 　教科書や地図帳にある「等時帯」は、これを基本として作られています。 ↓次へ　　↑もどる
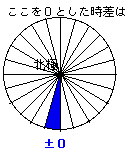
	例として、青でぬられた場所の時刻を基準に時差を考えてみましょう。 ↓次へ　　↑もどる
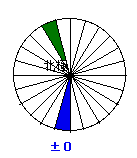
	青を基準（±０）とすると、緑のところは・・ ↓次へ　　↑もどる
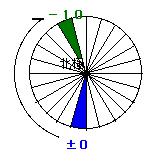
	右回りに１０、つまり−１０時間となります。 ↓次へ　　↑もどる
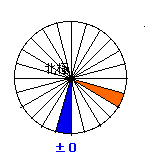
	オレンジのところは・・・ ↓次へ　　↑もどる
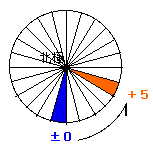
	右回りに５、つまり＋５時間になります。 ↓次へ　　↑もどる
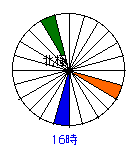
	もし青が１６時だとすると・・ ↓次へ　　↑もどる
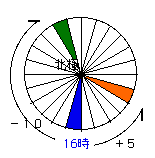
	緑は、１６時−１０ 　オレンジは、１６時＋５　だから・・・ ↓次へ　　↑もどる
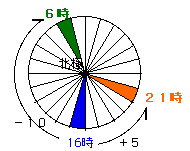
	６時と２１時、となります。 ↓次へ　　↑もどる
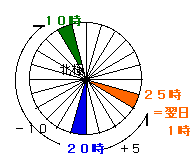
	もしも青が２０時なら、 　緑は、２０時−１０＝１０時です。 　オレンジは、２０時＋５＝２５時ですが、一日は２４時間ですから、くりあがって翌日の１時です。 ↓次へ　　↑もどる
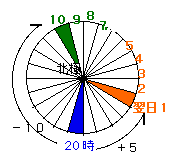
	ところで、この調子で進んでいくとどうでしょう。 　緑の方、左回りを続けていくと、９時、８時、７時とさかのぼっていきます。 　一方、オレンジの方、右回りを続けていくと、翌日の２時、３時、４時と進んでいきます。 ↓次へ　　↑もどる
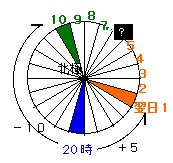
	はて。では、？のところは？ ↓次へ　　↑もどる
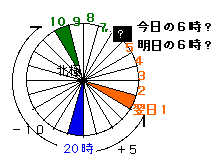
	右回りでいくと明日の６時。 　左回りでいくと今日の６時。 　どちらも正しくなってしまいます。 ↓次へ　　↑もどる
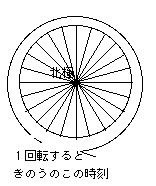
	そもそも、スタートまでたどってくるとどうでしょう。 　左回りに１回転すると、きのうのこの時刻になります。 ↓次へ　　↑もどる
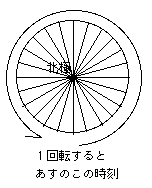
	右回りに１回転すると、明日のこの時刻になります。 ↓次へ　　↑もどる
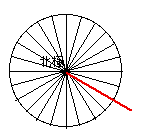
	こんな変なことになるのは、地球が丸くて終わりがないためです。 　そこで、無理矢理ですが「終わり」を決めます。ある経線を決めて、そこを越えては回らない、たどらないことにします。 ↓次へ　　↑もどる
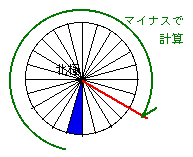
	この赤線までは、左回りで計算します。 ↓次へ　　↑もどる
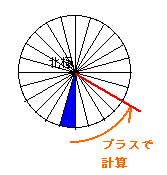
	この赤線までは、右回りで計算します。 ↓次へ　　↑もどる
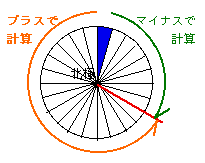
	スタートがどこになっても同じです。あくまで、この線をこえてはいけません。 　これで、時刻や日付は一つに決まります。 ↓次へ　　↑もどる
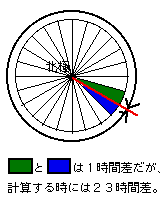
	この線の両側では、時刻は連続していますが、時差を計算する時にはこの線をまたげないので、ぐるりと地球を一周しなければいけません。 　当然、日付は必ず変わってしまいます。 　そこで、この線のことを「日付変更線」と読んでいます。 ↑もどる　　↑↑最初にもどる